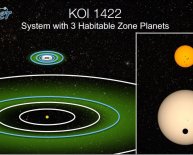
Astronomers Timeline

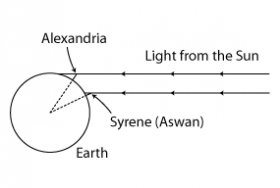
Eratosthenes estimates the radius of the Earth
The first steps were taken by Eratosthenes who combined reports of distances, in paces, from Aswan to Alexandria and then measured the difference in angle of the Sun above the horizon at noon (i.e. greatest angle) at the two places.
Copyrighted image Copyright: Used with permission
The circumference of the Earth is then [360 degs/angle difference] times the number of paces, and the radius is the circumference/[2 pi]. Solar parallax is then defined as [radius of the Earth/distance from Sun to Earth]

130 BC -
AD 1400
Stellar Geometry

Early star catalogues
Astronomy as a science cannot get started without star catalogues, and the first ones were produced a very long time ago and were remarkably accurate and reliable. (There were no lenses, and so no telescopes, but they used extremely long sighting lines). Two particularly dedicated early astronomers are Hipparchus (Greece, c.130 B.C.) - hence the HIPPARCOS satellite - and Ulugh Begh (Samarkand c. 1400, murdered because his colleagues were afraid of his knowledge).

Guesses of the distance to the Sun
Up to the mid seventeenth century there was agreement that the sun was remote from the earth. However, the various guesses made were all far too low (for example, the Greeks were off by a factor of 20) and based on woolly arguments such as what distance would fit in harmoniously with the sizes of the planets! Real measurements were first made from observations of the parallax of Mars, which can be made whenever it passes near to a bright (but distant and practically fixed) star. But they were not very consistent, other methods were needed.

Brahe
Tycho Brahe (1546- 1601), son of a Danish nobleman, was so struck as a child by an eclipse which occurred at the predicted time that he pledged his life to astronomy, and his family's wealth supported his work. He contributed to many areas of astronomy but there are two for which he is especially remembered. In 1572 he saw, and recognised the significance of, a bright new star, now known as Tycho's supernova. He also plotted the tracks of the planets with unprecedented care and passed the results on to one of his students, Johannes Kepler. The tracks are very complicated as seen from the moving platform of the Earth, but thanks to the accuracy of the data, Kepler was able to extract underlying simple rules of planetary behaviour, which Newton was able to explain through his even more fundamental laws of motion and gravity.

Kepler discovers the rules of planetary motion
Johannes Kepler assembled many years of planetary measurements, especially from Brahe, and found purely empirically (ie not deduced from an underlying theory) that they obey 3 simple rules, of which the one we need here is that planetary distances are proportional to the 2/3 power of their orbital period (their "year"). Or in symbols: T2 is proportional to R3.
Copyrighted image Copyright: Used with permission
The underlying laws are those of Newton, written in absolute terms but involving one of the six universal constants (see The Gravitational Constant). So measuring the planetary "years" - easy for the closer ones if not for the very distant ones - gives all the RATIOS of all distances. That is why it was so essential to measure one distance in absolute terms. We can then, quite literally, relate everything right back to the length of Eratosthenes' stride.

Newton's theories of dynamics and gravity
Newton greatly clarified the ideas of earlier scientists such as Galileo, and set them in mathematical form so that they had predictive power. He then created a theory of gravity and tested it on the Moon. In the process, Kepler's rules for the planetary orbits appeared as straightforward consequences of the laws. So his work is the mathematical structure behind all orbital analysis until the mid 20th century, when Einstein's general relativity cleared up some anomalies left by Newtonian analysis, and in its turn made predictions for extreme conditions such as neutron stars, for which Newton 's Laws fail to be even approximate.

Romer measures the speed of light
It's not hard to show the speed of light is very high (e.g. you and a friend with a horse; both have a lantern and a hat to put in front of it to make a signal - you can imagine the rest). But how fast? Infinitely fast? Ole Romer in 1676 used the satellites of Jupiter in much the same way as the lantern, with Jupiter as the hat. He discovered the timings of the satellite eclipses or transits changed as Jupiter came closer to us (or moved away), in our different orbits. He got 225, 000 km/sec - 30% too low, but showing clearly that it was not infinite.

Halley suggests using Venus' Transits to measure the Astronomical Unit
If we can triangulate any solar system body it gives the scale to the whole Solar System thanks to Kepler's Laws. So we want to choose the body closest to us which is orbiting the Sun, to give the best chance of getting a measurement. The candidates are Mars, any asteroid which comes within the orbit of Mars, and Venus. The crucial point is that it needs something as a backdrop against which to measure the chosen body. A frequent opportunity is given by watching Mars occult, or nearly occult, any distant star. Venus is inside Earth's orbit and so offers a special but rare opportunity when it passes between us and the Sun. The Sun itself provides the backdrop. We can then measure the distance of Venus and deduce the distance of the Sun. When it became possible to measure the distance of passing...